Introduction
The Bartender_LYSO project is a simulation of the waveform output from the MPPCs (SiPMs) of the LYSO calorimeter prototype, entirely written in C++ and utilizing the ROOT libraries. It's directly connected to the Geant4-based Monte Carlo simulation of the detector (see MC_LYSO for all details), as it simulates the digitizer and, consequently, the readout.
On these simulated data, it will be possible to test waveform analysis algorithms, searching for the best estimators for energy, time, and position, thus extracting a prediction of experimental resolutions.
This is only a very preliminary version, and several improvements are planned for the future. In addition to expanding its physical aspects (introducing SiPMs crosstalk, afterpulses, different sampling rates, jitter, and so on), there is an intention to enable a multithreading mode and set the output in ROOT format (likely, everything will be adapted for the use of RDataFrame).
The Waveform Construction concept
The final output waveform from a SiPM is constructed by summing single-photoelectron waves, one for each detected scintillation photon.
The analytical form of the 1-Phel waveform is described by a double exponential function:
\[ \text{Wave}_{1-Phel}(t) = -A \Bigg( \exp \Bigg( -\frac{t - t_{phel}}{\tau_{\text{RISE}}} \Bigg) - \exp \Bigg( -\frac{t - t_{phel}}{\tau_{\text{DEC}}} \Bigg) \Bigg) \theta( t - t_{phel} ) \]
where the parameter \( t_{phel} \) is the detection time of the scintillation photon, taken from the MC_LYSO data.
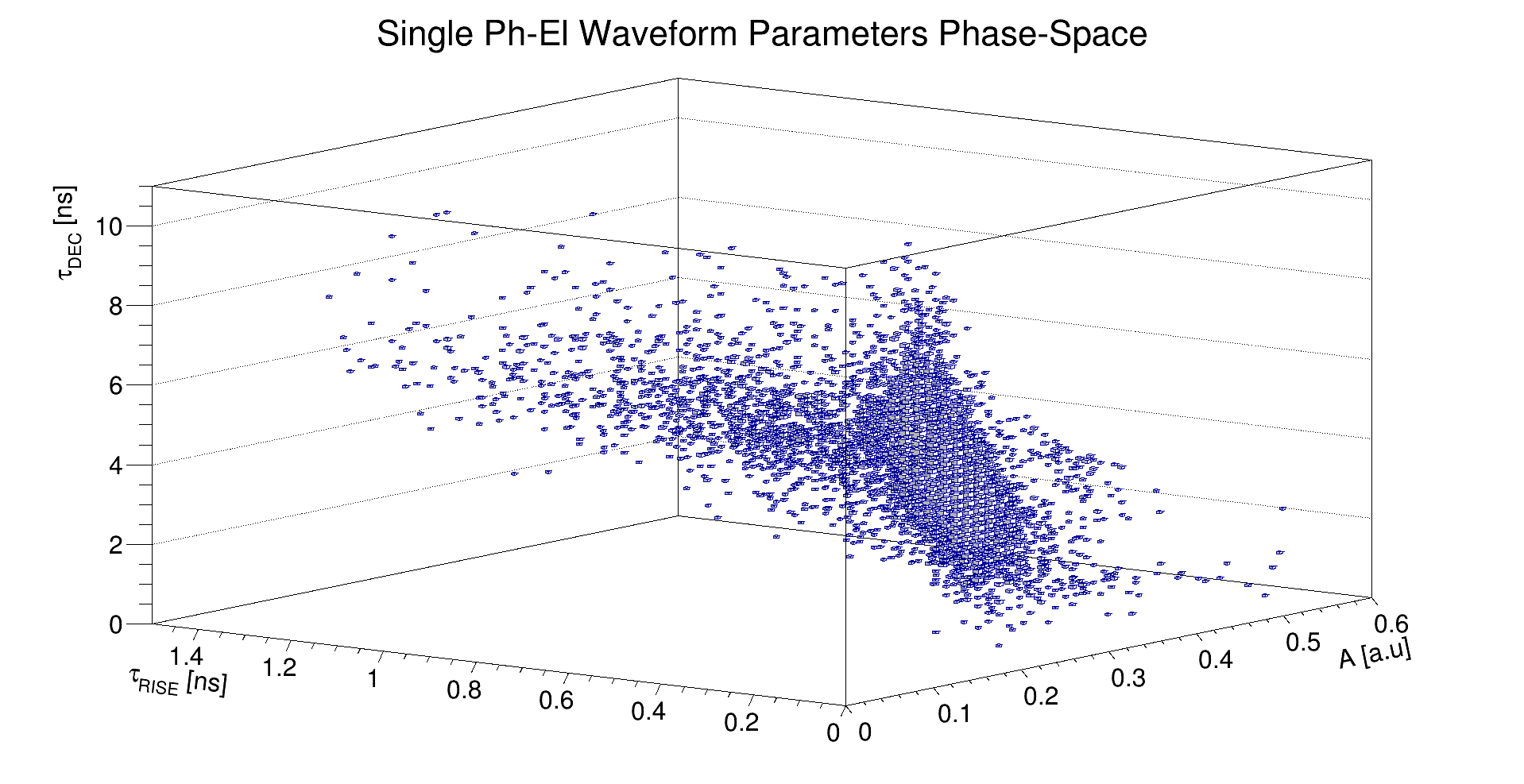
The parameters \((A, \tau_{\text{RISE}}, \tau_{\text{DEC}})\) are not fixed but fluctuate statistically (and are correlated with each other) for each 1-Phel waveform: the next two sections describe how the distributions and sampling of the parameters have been implemented.
Then, for \( N \) scintillation photons:
\[ \text{Wave}_{\text{SiPM}}(t) = \sum^{N}_{i} \Bigg[-A_{i} \Bigg( \exp \Bigg( -\frac{t - t_{phel, i}}{\tau_{\text{RISE}, i}} \Bigg) - \exp \Bigg( -\frac{t - t_{phel, i}}{\tau_{\text{DEC}, i}} \Bigg) \Bigg) \theta( t - t_{phel, i} )\Bigg] \]
To this, finally, Gaussian noise \( N(0, \sigma_{\text{Noise}})\) is added.
The Template for Parameters
The shape of the single-photoelectron waveform of a SiPM (and consequently its parameters) depends on the conditions of the acquisition electronics and the environment.
The chosen strategy is to provide the user with maximum flexibility by allowing them to choose the working point to simulate the SiPM response, providing a dataset directly.
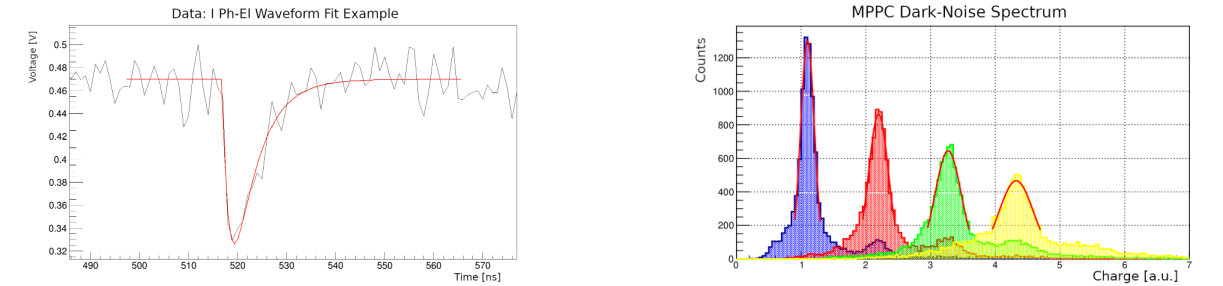
To test the method, signals produced by the dark noise electrons of an MPPC (Hamamatsu S13360-6050CS) were acquired. Subsequently, a best-fit was performed on each waveform, and the integral of the function was used as an estimator of the charge. From this, spectra were extracted (see image), and it was possible to identify the region of signals due to the first photoelectron.
In addition to the charge, all the best-fit parameters were saved in a text file (see How to run), which is then provided to Bartender_LYSO.
These parameters, through the method Bar::SetParsDistro(), populate a 3D histogram from which sampling occurs for each 1-Phel waveform using the TH3D::GetRandom3() method: this way, correlations between parameters are also taken into account.
Implementation and Flow of the Simulation
At the beginning of the application, the SiPM structure and the Bar class are instantiated, and the Bartender_Configure() function is called, which loads all user settings. The SiPM structure is responsible for containing user-provided information about the detector and its operating point, while Bar represents the "waveform generator".
Subsequently, the Bar::hPars histogram of parameters is filled by invoking the Bar::SetParsDistro() method.
Next, the Monte Carlo simulation ROOT file is accessed, and the eventID, hit count, collections of scintillation photon detection times, and their corresponding detector channels are extracted from the lyso TTree branches.
At this point, the core of the simulation begins.
Through the method Bar::InitializeBaselines(), the containers for the waveforms Bar::fFront and Bar::fBack are initialized with noise. They are pointer-to-pointer-to-pointer structures of type Double_t and represent 3D matrices [Bar::EVENTS]x[CHANNELS]x[SAMPLINGS]. This type of structure was chosen for two reasons:
- When the TTree lyso is read, the detector channels in the collection will arrive in random order, so the idea is to prepare the containers and update the waveforms in the corresponding "box" as needed;
- For optimization reasons, both in terms of memory and time, it does not make sense to manipulate the "entire function" (for example, TF1 objects), but it is better to work with the finite number of samples from the beginning.
However, in future versions, this system will definitely be deprecated in favor of a faster and more memory-efficient method.
Next, the event loop is executed, during which entries from the TTree are extracted. While looping over the entries of the collections of the two detectors, the methods Bar::SetFrontWaveform() and Bar::SetBackWaveform() are called one by one.
These functions receive as input the eventID, the channel number, and the detection time of the optical photon. They first sample the remaining parameters (see The Template for Parameters), and then add bin by bin the new 1-Phel waveform, evaluated using Bar::Wave_OnePhel(), to that present in the container at the selected indices.
At the end of the loop, the two containers are complete, and they are saved using Bar::SaveBar() on a text file BarID_[runID].txt.
Summary of the Bartender simulation
At the very end of the application, the function Bartender_Summary() is invoked. It creates (or updates) a file named Bartender_Summaries.txt where a summary of the simulation is written (the ID is the same as that of MC_LYSO). The recap is extracted from the macro file used (see the next paragraph) and includes all the information about the MPPC and its working point. Additionally, it records the date, user name and duration.
An example output is displayed:
How to run
To execute the simulation, you need to provide the ROOT file of the Monte Carlo simulation of the detector and a macro file for configuration, for example:
./bartender MCID_1707049321.root SiPM.mac
SiPM.mac is a ready-to-use template that must be modified with various settings. In this file, you also provide the path to the parameter files; it is mandatory for it to contain at least the following data in columnar format: the Fit status (0 if converged), charge, parameter \( A \), parameter \( \tau_{\text{RISE}}\), parameter \( \tau_{\text{DEC}}\), and the header for these must be:
Status/I:my_charge/D:A/D:Tau_rise/D:Tau_dec/D
to be correctly read by the function TTree::ReadFile(). A dataset is shown here.
Finally, the idea is that the user has reviewed the histograms of the best fit results and is able to establish, in addition to which charge cuts to apply to the spectrum, also the binning, minimum, and maximum for each of the 3 parameters through last settings shown in the mac.
Output Example
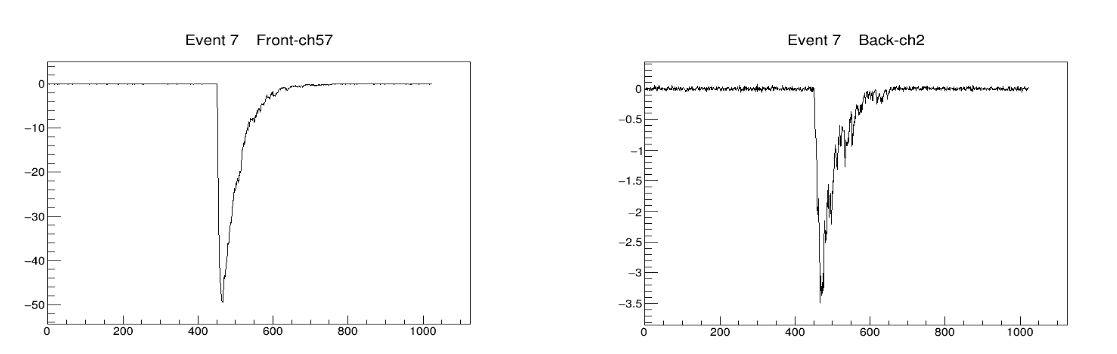
Given the non-optimized format of the output file, a macro is made available here to display the plot of the generated waveforms.
Executing from the root terminal
.L loadSamples.cc
you can use the function DrawSamples providing it with parameters (in order) the output file name, the eventID, 1 for Front detector or 0 for Back detector and the channel number.
For example:
DrawSamples("/home/lorenzo/MEG_Project/Simulazioni/Bartender_LYSO/build/BarID_1707049321.txt", 7, 1, 57)
or
DrawSamples("/home/lorenzo/MEG_Project/Simulazioni/Bartender_LYSO/build/BarID_1707049321.txt", 7, 0, 2)
The two waveforms are shown in the figure.
Generated by